Note from the author, 8 June 2020
The largest public demonstrations in a generation are at this moment demanding reform or abolition of the police in the United States.[a] The overwhelming and destabilizing violence by police against protesters has been egregiously disproportionate to the threats to property posed by a tiny minority of the demonstrators. Thanks to cell phone video and media coverage, Americans seem to be noticing, and there may be sufficient political momentum for meaningful change.
It is essential in this moment to remember how authorities will respond to this pressure. Always, those authorities will claim that their extraordinary powers are necessary to protect us from various threats, some real and others invented to fuel racist fantasies. Always, they will divert arguments about the unjust use of their awesome powers to blame their opponents and demonstrators. This week’s example is the police argument that damage to property justifies tear gas, indiscriminate beatings and the wholesale suppression of democratic guarantees of free speech and assembly. But according to many police officials, ‘a few’ – perhaps quite a few – abusive officers require no response, no civilian oversight, no one fired, no one even suspended, let alone prosecuted, no budgets reduced, no replacement of police powers with social services.
This cannot be acceptable in democracy. The Universal Declaration of Human Rights states in the preamble that ‘if man [sic] is not to be compelled to have recourse, as a last resort, to rebellion against tyranny and oppression, that human rights should be protected by the rule of law.’ That’s the deal. We consent to police powers because police promise to protect human rights and uphold the law, fairly and using only the minimum of force. We hold the police accountable for the use of their massive powers because unjust violence by the state threatens the basis of our entire society. We hold the state, we hold police and soldiers, to a far higher standard than we hold citizens because there is so much at stake.
This article was originally published in 2016 based on a statistical analysis led by Dr Kristian Lum. It was largely a response to the demonstrations demanding justice for the 2014 police killing of Michael Brown in Ferguson, Missouri – and to the government’s tiny and ultimately inconsequential effort at reform.
For generations, black Americans have demanded reform: law enforcement’s unjust violence against their community must stop, and the offending officers must be prosecuted. There has been little if any improvement. As white supremacists have infiltrated US law enforcement in recent years, policing against black Americans may well have become even less just. For the moment, non-black Americans are paying attention. I pray that this time we will see meaningful change in US policing.
– Patrick Ball
Police Homicides in the United States
Americans are afraid of many threats to their lives – serial killers, crazed gunmen, gang bangers, and above all terrorists – but these threats are surprisingly unlikely.[1] Approximately three-quarters of all homicide victims in America are killed by someone they know.[2] And the real threat from strangers is quite different from what most fear: one-third of all Americans killed by strangers are killed by police.
This is the story of the hidden numbers of police homicides in the United States. The killings of Michael Brown, Eric Garner and Walter Scott have increased the world’s attention to US police violence, yet most Americans underestimate the threat posed by the people charged with keeping them safe.
Let’s turn to the facts.
There is no national registry of civilians killed by police and corrections officers in the United States. Several states, including Texas, Connecticut and California, maintain complete records, but in most parts of the United States, local law enforcement chooses whether to report officer-involved homicides to the federal government. The lack of systematic data poses a challenge both for those who wish to hold police accountable for their actions and for those who want to propose reform measures to reduce police violence. How many killings are committed by police?
In recent months, a number of ‘crowdsourced’ databases have emerged, including in particular Fatal Encounters and Killed by Police.[3] Journalistic efforts, including those by the Washington Post and the Guardian, have conducted infographic-style analyses of the patterns of police homicides that are known to the public. This latter qualification is a big one.
For the past twenty-five years, my colleagues and I have documented mass killings by state agents in over thirty countries around the world. From El Salvador to South Africa, from Kosovo to East Timor, from Colombia to Congo, we have built databases and conducted statistical analyses of patterns of violence by governments on behalf of tribunals, truth commissions, UN human rights missions and for local human rights activists. One of the only constants across all these examples is that the data we are able to collect is always partial.[4]
It is difficult to collect information about violence committed by governments. Victims are afraid of retaliation and so they explain the deaths in other ways. The families of victims rightly recognize that to accuse a police or military officer of murder puts themselves and their family members directly in the path of well-resourced and sometimes violent adversaries who may be above the law.
Furthermore, state agents who commit mass violence make every effort to disguise their actions. They influence coroners to describe the killings as accidents. They create narratives that distort responsibility so that it seems as though the victim is at fault for his or her own death. In their own narratives, police and military officials are keeping the peace and protecting innocents from the violent, the rebellious and the criminal. And in many cases, these narratives are correct. After all, the reason we consent to the existence of armed forces in our midst is precisely to keep us safe from these threats.
In other incidents, however, the police have killed people by accident, or because they used excessive force, or because their rules of engagement permit them to use deadly force whenever they feel their lives are threatened, for any reason. The question Americans face is therefore at what point the violence committed by our protectors exceeds the violence we might suffer from the people they claim to be protecting us against?
The FBI maintains a list of homicides called the Supplementary Homicide Report (SHR), which includes people killed by police and corrections officers. Crucially, the SHR only includes homicides committed by police that in the judgment of the police department or the local FBI have been justified, that is, considered legal. Many people, including members of Congress, have asked the larger question: How many people in total are killed by the police in the United States every year?
Seeking an answer, Congress passed the Death in Custody Reporting Act of 2000, requiring the Department of Justice to maintain a list of people killed by police in the United States. The Arrest-Related Deaths program (ARD) was created by the Bureau of Justice Statistics to do this. After several years, the Bureau of Justice Statistics (BJS) decided to conduct an assessment of the coverage of the Arrest-Related Deaths database. Was this database complete, or did it omit victims?
The BJS faced the same problem looking at the victims of police homicides in the United States that the global human rights community faces when we try to figure out how many people have been killed in Syria’s civil war: we have a number of lists which partially overlap, and which are individually and in sum incomplete. It turns out that there is a statistical technique specifically designed for data of this kind – using multiple, independently collected lists – that can create good estimates of how many people are not on the lists.
The Bureau of Justice Statistics turned to Research Triangle Incorporated, a North Carolina-based statistics think tank, for help with this statistical evaluation. They issued a report published in March 2015 that compared the Arrest-Related Deaths database with the FBI’s Supplementary Homicide Report.[5] The report considers homicides committed by police within the years 2003–2009 and 2011 (2010 was omitted). They first asked how much the two databases overlap, that is, how often they document the same victims.

The left circle shows the number of deaths documented in the Arrest-Related Deaths database, and the right circle shows the deaths documented by the Supplementary Homicide Report. The overlapping section in the middle – the intersection of the two lists – shows the number of deaths on both lists.
Notice that in the Venn diagram, the two lists are encircled by a large cloud of smoke – think of this as the ‘universe’ of total deaths, which includes the deaths that are not on the ARD or SHR lists.[6] That is, the cloud includes deaths that are not observed by these projects. We can use some probability theory and algebra to estimate the number of deaths not on the lists, and this is an important insight. The cloud refers to the total number of police homicides that can be ‘statistically inferred’ to exist.
Here is an analogy for how this statistical technique works. Imagine that there are two rooms, and we want to know which of the two is larger. Our only tool for assessing the rooms’ sizes is a handful of small rubber balls. The balls have the curious property that when they strike each other, they make a distinctive clicking noise. We take the rubber balls, throw them into the first room and listen – click, click, click. Then we gather the balls and throw them into the second room – click. Which room is larger?
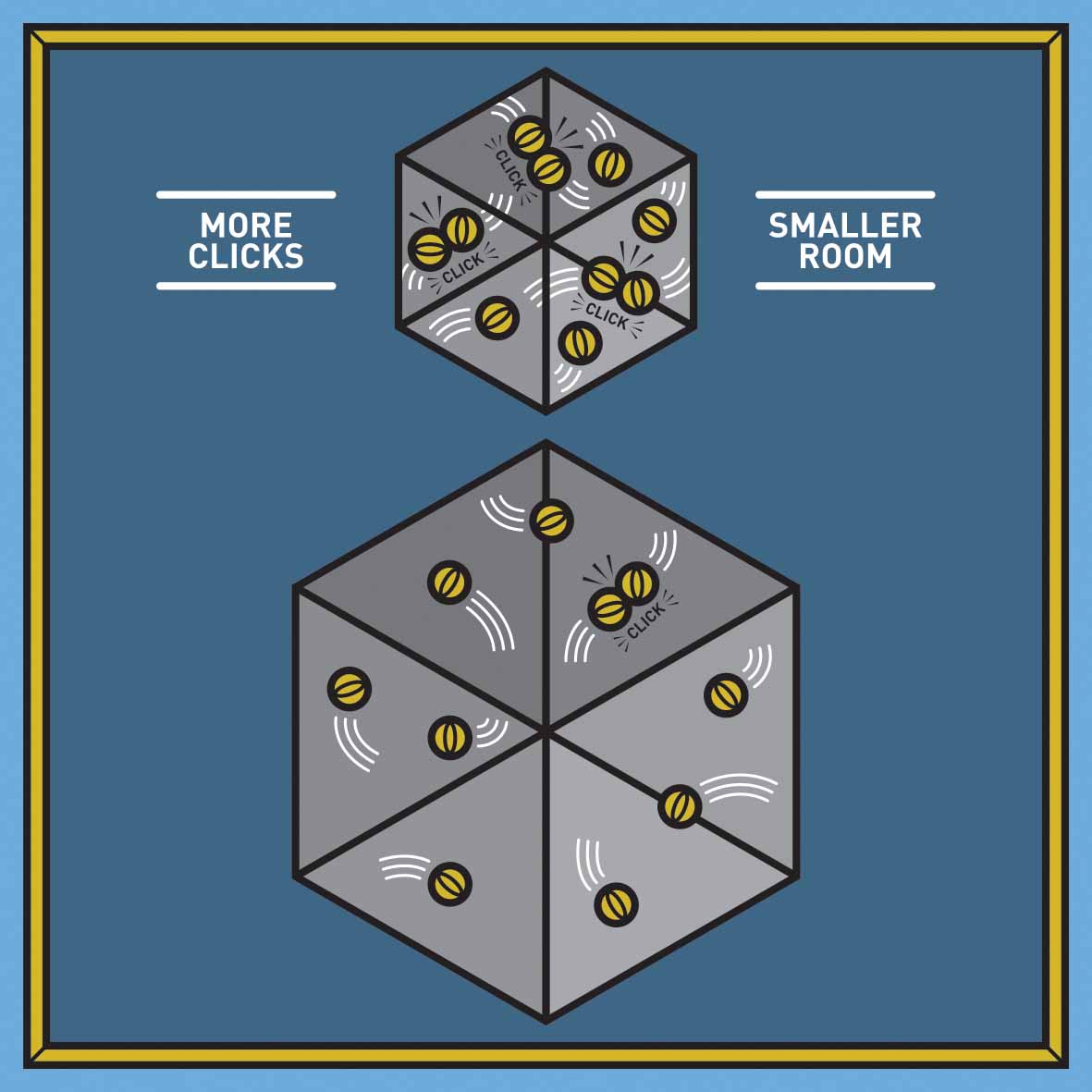
The second room is larger. The smaller room forces the balls together more closely than the larger room, so the balls have less room to bounce around, and they therefore hit each other more often.
What the BJS analysts have done in their report is akin to throwing the two databases into the ‘room’ of all police homicides in the United States. It turns out that the ratio of the sizes of the individual databases to the number of times they collide can provide an estimate of the total number of police homicides in the US – including those that have not been observed.
In my opinion, this is the real purpose of statistics. We often use simple statistics that just count things, like how many widgets our factory shipped last year. But statistics is much more useful when it enables us to know something about uncertainty. If we have a measure that we know to be imprecise, how imprecise is it: wildly, or only slightly? If we have a measure that systematically undercounts something (statisticians would call this bias), is the undercount minimal, or is it severe? Can we correct the bias? These are the kinds of questions that statistics can answer. In this case, the estimate made by the Bureau of Justice Statistics is much closer to the likely true number of homicides committed by police than the raw data, but it can be improved considerably. To understand how this works, let’s dive into the technical bits.
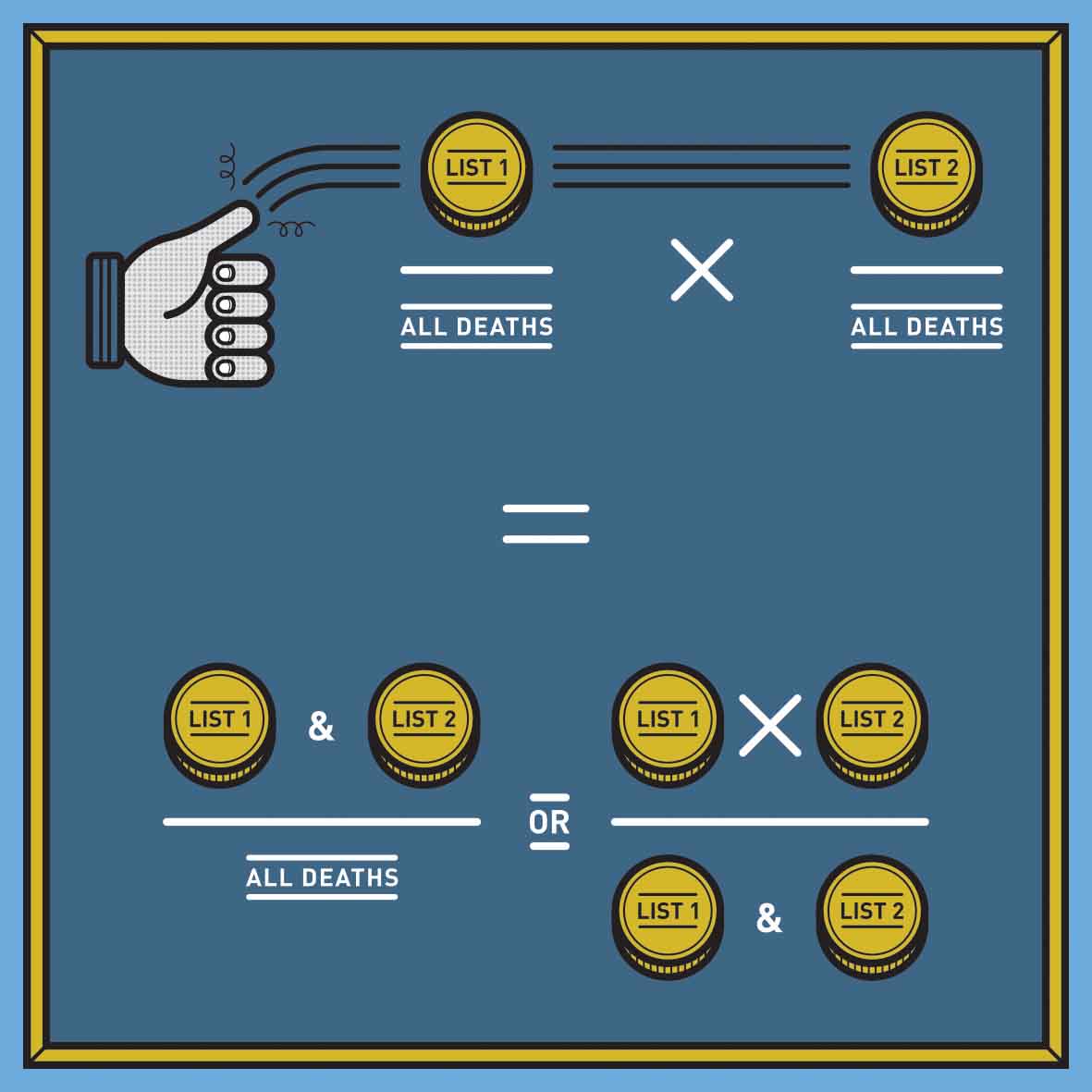
Here’s the math behind measuring undocumented police homicides: there is a total number of homicides committed by police in the United States, denoted by an uppercase N. The uppercase N represents all the deaths in the cloud, but we don’t know what it is. What we do know is the number of deaths listed, documented, and known in the Arrest-Related Deaths database – call this number A; the list of deaths documented and known by the FBI in the Supplementary Homicide Report – call this B; and the number of deaths known in both databases – we’ll call this M. The probability that any given death in N is documented by the Arrest-Related Deaths database is A divided by N; that a death in N is documented by the FBI’s Supplementary Homicide Report is B divided by N; and that a death is documented by these two lists, M divided by N.
But here’s where we can really get some leverage. Let’s think about tossing coins: with one coin, the probability of a flip coming up heads is one over two. If I flip two coins, the probability that I’ve thrown two heads is one over four, that is, it equals the probability of the first head multiplied by the probability of the second head.
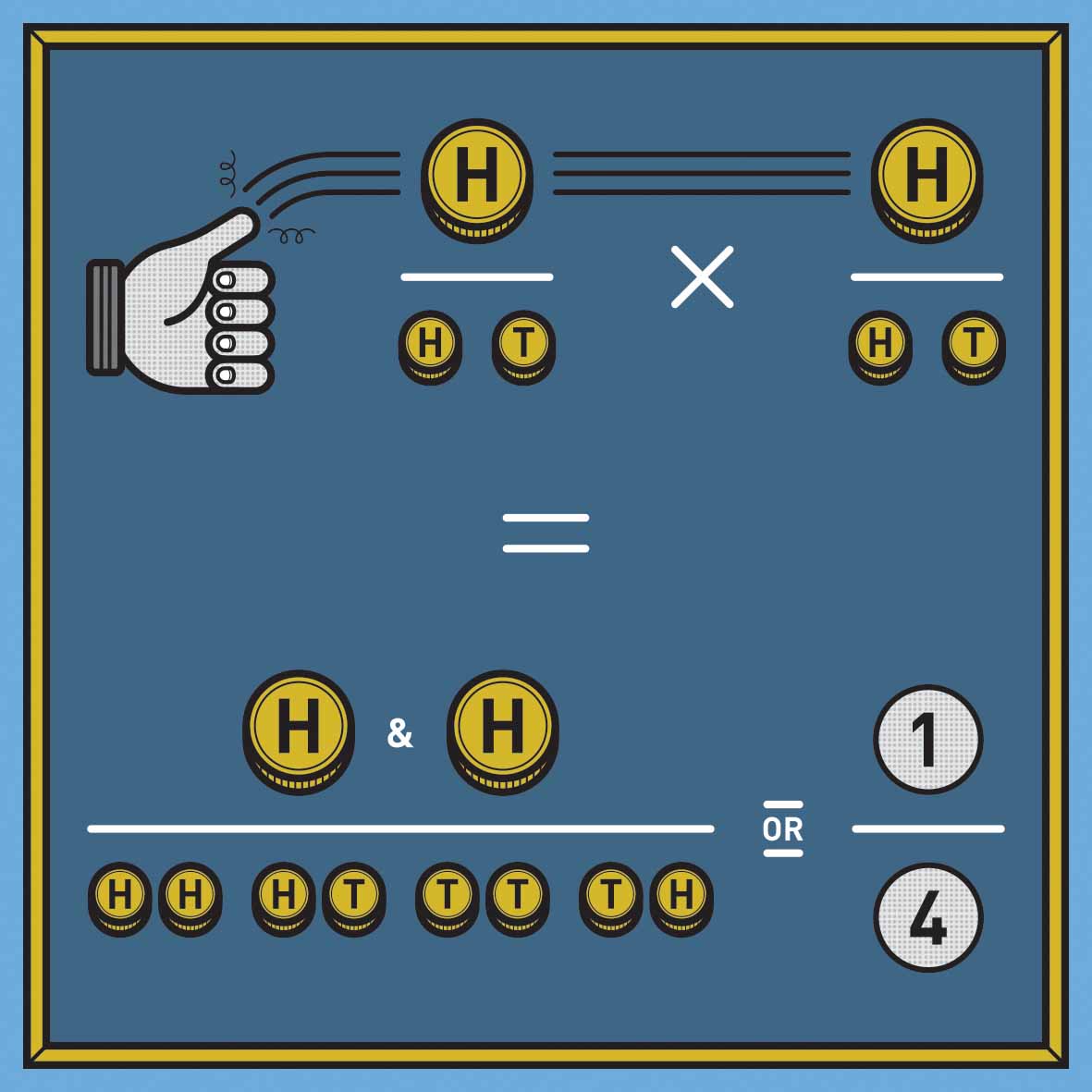
Applying this logic to the lists is essentially the same. Remember that we know the number of people on both lists (M), so the probability of being documented by both lists is M/N. As with the probability of two heads in a coin toss, this probability is also equal to the probability of being on the first list (which we defined as A/N) multiplied by the probability of being on the second list (which is B/N).
From this, we can say that M/N = A/N x B/N. This is an equation with one unknown, N, because we know A, B and M; that means we can solve for N. Our best estimate of N – the total universe of homicides – is therefore AB/M, or the number of victims listed in the Arrest-Related Deaths database multiplied by the number of victims listed in the Supplementary Homicide Report divided by the number of victims recorded in both.
This is one way that statistics illuminates uncertainty: it provides a model based in probability theory to tell us what we don’t know. This is what the Bureau of Justice Statistics analysts have done to estimate the total number of police homicides as 7,427. That is, they estimate that in addition to the homicides documented by the Arrest-Related Deaths database and the Supplemental Homicide Report, an additional 2,103 victims were killed by police in the United States during the period 2003 through 2009 and 2011 (excluding 2010).
The Bureau of Justice Statistics released their report in March 2015, and it created a media tizzy. Pundits and politicians were reminded that even the federal government doesn’t know how many people in America are killed by police. It was a striking admission of the weakness of the federal bureaucracy with respect to recalcitrant local law enforcement officials who refuse to publicly share the most basic facts about potential abuses.
But as bad as the news of this report was, the reality is even worse.
To understand why, we need to return to the metaphor of the rubber balls used to measure the size of different rooms. Remember that we were able to estimate the relative sizes of the rooms because in the larger room, the balls hit each other less frequently. There is an assumption hidden in that idea: that the balls travel freely through the air in the rooms.
But what if this assumption isn’t true? What if, for example, some of the balls tend to be attracted to each other, so that when they are nearby, they veer toward each other, bounce against each other, and create a click? If this were true, we would hear many more clicks than we would if the balls were flying around without attracting each other. We would inaccurately infer that the room is smaller than in fact it really is. This is what happened with the Bureau of Justice Statistics report.
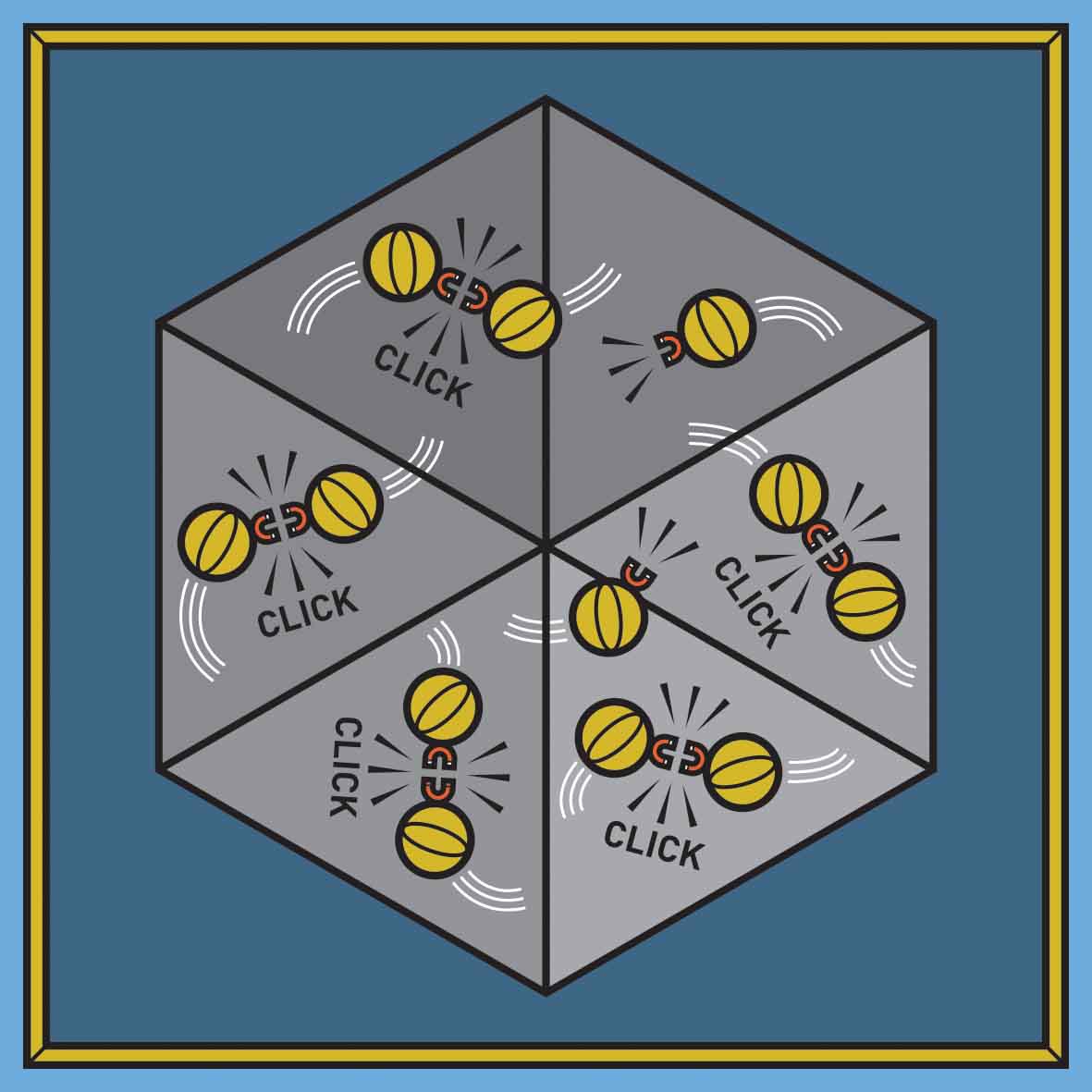
When a middle-class person is killed by police, or when a person is killed by police in front of bystanders taking videos on phones, the media tend to report about this event very thoroughly. In circumstances like these, the police are very likely to report this case to the FBI because they know the FBI will hear about it. These cases are like the balls that tend to attract each other.
Conversely, if a person is killed by police without the presence of witnesses, and is from a social network of people fearful of retaliation by police, local police may know that they don’t have to report this to the FBI. For the same reasons, this person’s death might also remain undocumented by local media. This is the kind of killing that is unlikely to be reported at all.
These two examples show that if one source reports a given killing, the other source is also likely to report it. But if one source overlooks a killing, the other source is similarly likely to overlook it. In statistical terms, we say that the probability of reporting (or not) to the FBI – and therefore by the Supplementary Homicide Report – is positively correlated with the probability of reporting (or not) by the media or other sources recorded in the Arrest-Related Deaths database.
One result of this correlation is that our equation for estimating the total deaths – AB/M – is inaccurate because M is too large. The balls are not traveling freely through the room and striking each other only when they cross paths; instead many balls are drawn together and strike each other more frequently than expected. And if the intersection of our Venn diagram (M) is too large, our estimate of total deaths (N) is too small.
This is a standard problem with this statistical approach,[7] and we have calculated variations of this math in many contexts, including our study of genocide in Guatemala’s armed internal conflict, ethnic cleansing in Kosovo, killings in Perú’s civil war, homicides and lethal violence more generally in Colombia’s civil conflict, and killings in Syria’s ongoing war. In these projects, we are acutely sensitive to the problem we have here. In statistical language, this is called ‘list dependence,’ and there are decades of research done by mathematical statisticians that help correct estimates by measuring the strength of the attraction among the balls.
One way to understand this is that if we have three or more lists, we can measure the attraction between any pair of lists. With two lists we have no way to know what the correlation between the lists might be. With three or more lists, though, we can measure the attraction among the balls directly, and then account for that attraction to arrive at a much more accurate estimate.
What my colleague Dr Kristian Lum and I did is to ask: what are these two lists?[8] One is a list maintained by police. The other is a list of people reported in the media. We’ve used lists like this before. Many times. Many, many times.
In all our previous work in other countries, we used three, four, five, or more lists, and because we used three or more lists, we could calculate what the correlations were between all the pairs of lists in each country. Remember, the correlations are just numbers. So we asked ourselves: what is the usual range for correlations in similar scenarios? The answer is shown in the graph below, titled ‘Estimated Pairwise List Dependence.’ The range shows the correlations we have found among many pairs of lists of homicides in five countries. The higher the number at the bottom, the higher the correlation. The wider the bar, the larger the range of observed correlations. The lines extend left and right showing the most extreme values.
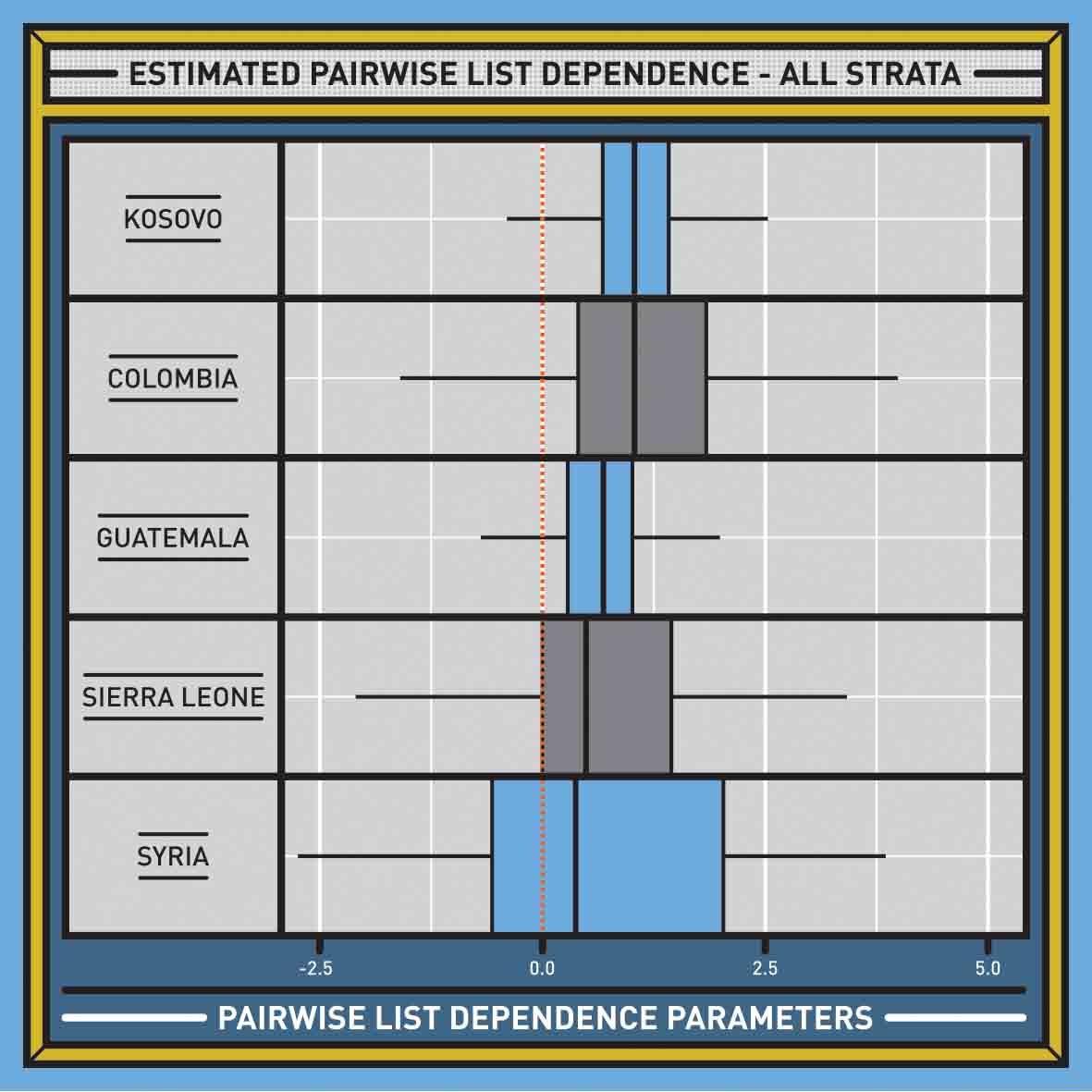
We don’t know the correlation between the Arrest-Related Deaths database and the Supplementary Homicide Report. We have only two lists, and consequently we can’t measure the correlation. But with the countries listed in this graph, we can draw an insight to what the correlation between the sources in the United States might look like. And with a possible correlation, we can adjust the estimate of US police homicides accordingly.
Let’s turn to the second graph, titled ‘Estimates of Total Deaths by Country’s List Dependence.’ This graph modifies the estimate of total police homicides given by the Bureau of Justice Statistics by asking the question: what would their estimate look like if the correlation between the two lists we have were like the correlations found among lists in these other countries? The BJS estimated 7,427 total police homicides. If we take into consideration the correlation between the two lists (that is, the attraction among the balls thrown into the room), how much would the estimate increase?
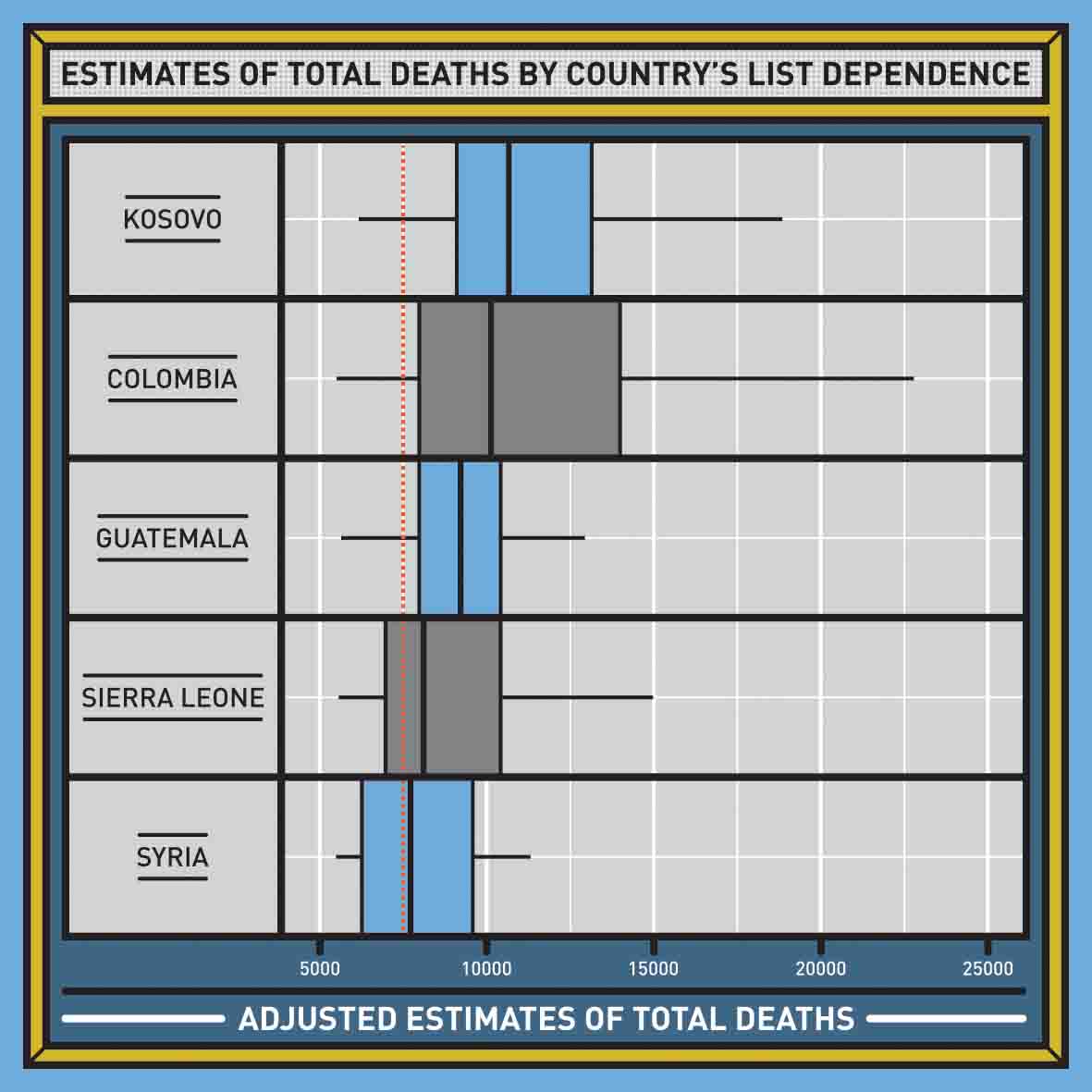
The bars in this graph show the range of estimated homicides if the correlation for the US sources were like the ranges we’ve found in the countries listed in the left-hand column. If the US correlation were like the correlations among sources in Kosovo, the estimate would be a bit more than 10,000 US police homicides. If the US correlation were like the correlations among sources in Colombia, the estimate would be a bit less than 10,000. And so forth.
To understand the impact of the correlation between one list organized by the police – like the Supplementary Homicide Report – and another list organized from media sources – like the Arrest-Related Deaths database – it’s most useful to compare them to other cases where we have similar kinds of lists, that is, police and media lists. And the range of correlations that are most informative for our investigation are those in Colombia, where there is a very effective police reporting database, and good databases maintained by human rights groups of homicides reported in the press.
Using the correlations from these lists, we conclude that for the eight-year period included in the study by the Bureau of Justice Statistics, it is likely that there were approximately 10,000 homicides committed by the police, that is, about 1,250 per year. Keep in mind that the Bureau of Justice Statistics report itself excludes many jurisdictions in the United States that openly refuse to share any data with the FBI. The true number of homicides committed by police is therefore even higher. Though not a true estimate, my best guess of the number of police homicides in the United States is about 1,500 per year.
As I said at the beginning of this article, the estimate of 1,500 police homicides per year would mean that eight to ten per cent of all American homicide victims are killed by the police. Of all American homicide victims killed by people they don’t know, approximately one-third of them are victims of the police.
America is a land ruled by fear. We fear that our children will be abducted by strangers, that crazed gunmen will perpetrate mass killings in our schools and theaters, that terrorists will gun us down or blow up our buildings, and that serial killers will stalk us on dark streets. All of these risks are real, but they are minuscule in probability: taken together, these threats constitute less than three per cent of total annual homicides in the US.[9] The numerically greater threat to our safety, and the largest single category of strangers who threaten us, are the people we have empowered to use deadly force to protect us from these less probable threats. The question for Americans is whether we will continue to tolerate police violence at this scale in return for protection against the quantitatively less likely threats.
This research was previously published as a blog post and in a white paper published by the HRDAG.
[a]: For an excellent set of reform proposals, see Campaign Zero. For a review of good thinking about replacing the police with alternative mechanisms for civil peace, see this collection of articles by The Marshall Project.
[1] Less than 1% of all homicides involve three or more victims. See Cooper, A., and E.L. Smith, ‘Homicide Trends in the United States, 1980-2008,’ US Department of Justice, Bureau of Justice Statistics (NCJ 236018), November, 2011, p. 24.
[2] See, Cooper and Smith op. cit., Table 8. Note that for 36–44 per cent of homicides during this period, the victim-perpetrator relationship is unknown. Local law enforcement may not have reported the relationship, or the perpetrator may be unidentified. Case-based research on unknown victim-perpetrator relationships suggests that there is little or no bias caused by the missing data. See, e.g., Quinet, K., and S. Nunn, ‘Establishing the Victim-Offender Relationship of Initially Unsolved Homicides: Partner, Family, Acquaintance, or Stranger?’ Homicide Studies.
[3] See an analytic merge of these two databases at MappingPoliceViolence.org
[4] See the project list here and the publications here.
[5] Banks, D., L. Couzens, C. Blanton, D. Cribb, ‘Arrest-Related Deaths Program Assessment Technical Report,’ RTI Interational (NCJ 248543), March 2015.
[6] The estimate made by the BJS is slightly more complicated than the simple algebra shown here, so their estimate of the total number of police homicides (7427) is a little larger than the direct estimate ((1939+1681)*(1704+1681)/1681 = 7290). See their [section 3.1, p.13](http://www.bjs.gov/content/pub/pdf/ardpatr.pdf) for details.
[7] The canonical reference for this method is Bishop, Y., S.E. Fienberg, and P. Holland, Discrete Multivariate Analysis, MIT Press. 1975, especially chapter 6.
[8] For all the math, see Lum and Ball, op. cit. https://hrdag.org/wp-content/uploads/2015/07/2015-hrdag-estimating-undoc-homicides.pdf
[9] Mass killings represent less than one per cent of annual homicides; terrorists kill many fewer Americans than that; and although the total number of deaths due to serial killers is debated, the usual citation suggests it is less than one per cent of annual homicides. See Kiger, K. ‘The darker figure of crime: The serial murder enigma.’ In S. Egger (Ed.), Serial murder: An elusive phenomenon (pp. 35-52). New York: Praeger. 1990. Additional serial killer victims are likely among the ‘missing missing,’ that is, undocumented homicides which appear in neither the numerator nor the denominator of any homicide rate. See Quinet, K., ‘The Missing Missing: Toward a Quantification of Serial Homicide Studies.’ Homicide Studies. 11(4): 319-339. 2007.
Feature photograph © Diana Robinson. Illustrations by Greygouar.







